Prénoms et réussite au bac

Le sociologue Baptiste Coulmont, auteur de Sociologie des prénoms, s'est intéressé aux corrélations entre le prénom des candidats au baccalauréat 2012 et leur réussite à cet examen (voir ici pour l'étude originale sur le blog de l'auteur). Ce travail a été largement relayé par les médias, car les résultats sont particulièrement intéressants. Il s'avère que certains prénoms réussissent mieux que d'autres: les Madeleine et autres Côme réussissent bien mieux (plus de 25% de mentions TB chez ces candidats) que les Youssef ou Nabil (aucune mention TB cette année). Ce n'est probablement pas le prénom en lui-même qui influe sur le résultat, mais plutôt le fait que le prénom est souvent le reflet de certains critères sociologiques (classe sociale, origine géographique, profession des parents...). Ce sont ces derniers critères qui ont une influence certaine sur les résultats scolaires, démontrant des inégalités profondes dans le système éducatif actuel.

EDIT: maintenant, vous pouvez connaître les résultats des candidats portant votre prénom!

J'ai voulu effectuer quelques analyses complémentaires sur ces mêmes données, en m'intéressant plus aux aspects mathématiques que sociologiques. Il peut s'agir d'un exemple intéressant dans l'enseignement d'un cours de probabilité et statistiques, illustrant notamment les notions de conditionnement, d'espérance conditionnelle, de raisonnement bayésien, ou de divergence de Kullback-Leibler.

Résultat moyen en fonction du prénom

Nous nous intéressons au profil de résultats: il s'agit d'une courbe donnant la proportion de candidats pour chaque résultat possible: oral (O), passable (P), mention assez bien (AB), mention bien (B), mention très bien (TB). Cela s'appelle aussi une distribution de probabilité sur l'ensemble des résultats possibles. Voici le profil moyen, pour tous les candidats et indépendamment du prénom. Il y a environ 17% de candidats devant passer l'oral, 35% de P, 27% de AB, 14% de B, 7% de TB. Rappelons que ces chiffres comportent deux biais: il ne s'agit que des candidats ayant obtenu l'examen après le premier écrit, ou ayant obtenu la possibilité de passer l'oral. Les candidats ayant échoué après le premier écrit ne sont pas inclus dans les données. Le deuxième biais concerne le fait que seuls les candidats ayant accepté de diffuser publiquement leurs résultats sont inclus.

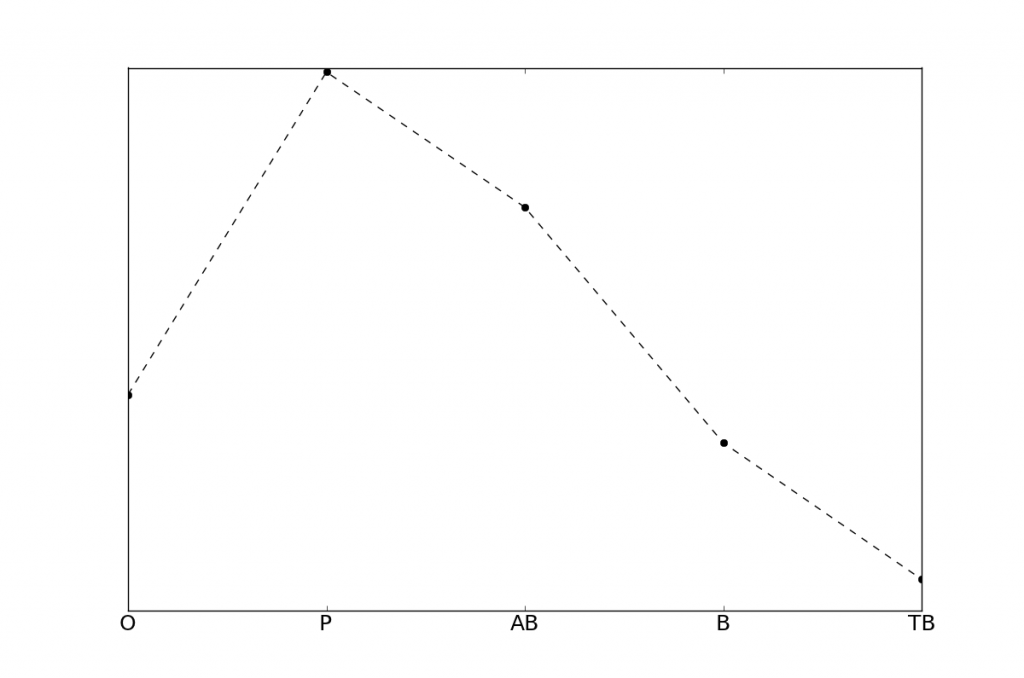
Maintenant, nous nous intéressants à l'influence du prénom sur le résultat au bac. Nous allons utiliser deux approches mathématiques: la première utilise l'espérance conditionnelle, la seconde utilise la divergence de Kullback-Leibler. Dans les deux cas, l'idée est de comparer le profil moyen avec le profil pour chaque prénom. Cela revient à étudier la distribution de probabilité conditionnelle à la donnée du prénom. En d'autres termes, si un candidat pris au hasard a 7% d'avoir eu mention TB, le fait de savoir qu'il s'appelle Côme, Nicolas, ou Youssef change-t-il cette probabilité? Cette question correspond au principe mathématique de conditionnement. Du point de vue de l'espérance conditionnelle, on peut se demander, si la moyenne générale au bac est de 12 chez tous les candidats, combien de points en plus on peut attendre chez un candidat en connaissant son prénom? D'un point de vue bayésien, on peut aussi voir la question ainsi: connaissant le profil de résultat moyen (prior), le fait de connaître le prénom change-t-il le profil de résultat (posterior)?

Moyenne au bac

Dans cette première approche, nous nous intéressons à la moyenne des candidats, sachant ou non leurs prénoms. Mathématiquement, il s'agit respectivement de l'espérance de la distribution moyenne du résultat, et de l'espérance conditionnelle de cette distribution sachant le prénom du candidat. Pour cela, nous assignons d'abord une note moyenne à chaque mention: 9 pour O, 11 pour P, 13 pour AB, 15 pour B, 17 pour TB. Il ne s'agit bien sûr que d'une approximation, puisque nous n'avons accès qu'à la mention et pas à la note moyenne de chaque candidat. Chez tous les candidats (ayant réussi ou devant passer l'oral, donc), la moyenne globale est de 12.2.

Nous pouvons ensuite, pour chaque prénom, calculer l'écart, par rapport à cette moyenne, de la moyenne des candidats portant ce prénom (ou espérance conditionnelle). Nous trouvons que cet écart varie entre -2.1 (Nahida) et +2.1 (Gaëtane), soit une bonne mention d'écart. Autrement dit, une Nahida a en moyenne une mention en-dessous de la mention moyenne des candidats, comparé à une mention au-dessus pour une Gaëtane. Voici le profil de résultat des six prénoms les plus en-dessous de la moyenne:

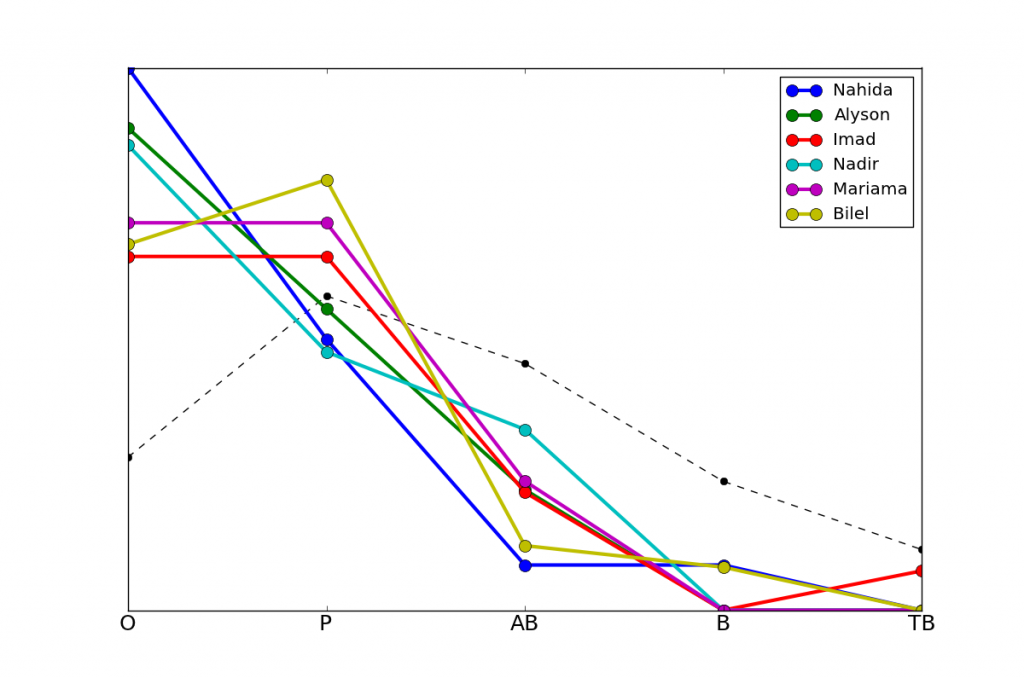
Voici les résultats complets pour les 30 prénoms les plus en-dessous, avec l'écart à la moyenne.

Nahida       -2,07
Alyson       -1,97
Imad         -1,91
Nadir        -1,80
Mariama      -1,75
Bilel        -1,65
Fatma        -1,63
Abdelkader   -1,60
Manuella     -1,59
Aziza        -1,57
Yassin       -1,57
Mounir       -1,57
Moussa       -1,56
Siham        -1,55
Patrice      -1,53
Kamel        -1,53
Giovanni     -1,53
Dalila       -1,47
Abdel        -1,45
Erwin        -1,42
Nordine      -1,41
Khalid       -1,40
Latifa       -1,40
Youssef      -1,38
Sofian       -1,38
Souad        -1,37
Soumia       -1,37
Bilal        -1,36
Alysson      -1,36
Lamia        -1,35

Du côté des prénoms avec l'écart le plus au-dessus de la moyenne, voici les profils de résultats.

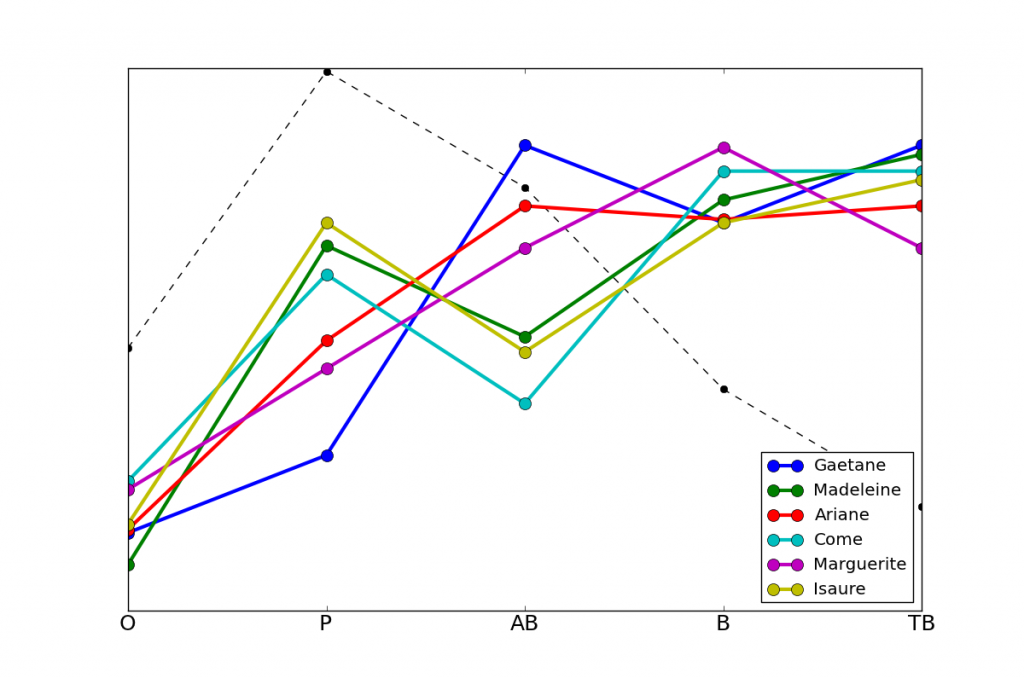
Gaetane        2,13
Madeleine      1,94
Ariane         1,82
Come           1,76
Marguerite     1,73
Isaure         1,71
Mahaut         1,61
Marie-Anne     1,58
Hannah         1,51
Melisande      1,46
Viviane        1,45
Quitterie      1,43
Marie-Astrid   1,43
Guillemette    1,38
Anouk          1,35
Irene          1,34
Blaise         1,33
Arielle        1,33
Solange        1,33
Leon           1,31
Domitille      1,29
Celeste        1,23
Noemi          1,23
Cleo           1,23
Hortense       1,22
Baudouin       1,19
Jack           1,19
Iris           1,17
Jolan          1,17
Gaspard        1,16

Destin des prénoms

Avec la seconde méthode, nous nous intéressons à la quantité d'information obtenue avec la connaissance du prénom. Autrement dit, posons-nous d'abord la question suivante:

• Quel résultat attendre d'un candidat pris au hasard?
• Réponse: voir le profil de résultat moyen au début de cet article, supposé connu a priori (7% de mention TB, 14% de mentions B, etc.).

Ensuite:

• Quel résultat attendre d'un candidat pris au hasard, si l'on nous donne son prénom? Plus précisément, à quel point notre attente du résultat est-elle modifiée par la connaissance de son prénom?
• Réponse: la divergence de Kullback-Leibler entre la distribution moyenne, et la distribution conditionnée au prénom, donne une réponse quantitative à cette question.

Cette divergence constitue une sorte de métrique entre deux distributions. Une divergence quasi-nulle signifie que les distributions sont quasi-identiques, donc que notre attente du résultat n'est pas modifiée par la connaissance du prénom. A l'inverse, une divergence plus élevée signifie que la connaissance du prénom change de manière importante le résultat que l'on peut attendre du candidat (voir ici pour des détails). Les graphiques ci-dessous illustrent cela.

Voici d'abord les six prénoms associés à la divergence la plus élevée. Nous reconnaissons les prénoms obtenus plus haut, sauf que les prénoms réussissant le mieux sont mélangés avec ceux réussissant le moins. En effet, cette mesure signifie à quel point les profils de résultats sont différents de la moyenne, mais pas la direction de cette différence, qui peut être meilleure (plus de bonnes mentions) ou moins bonne (plus de mauvais résultats).

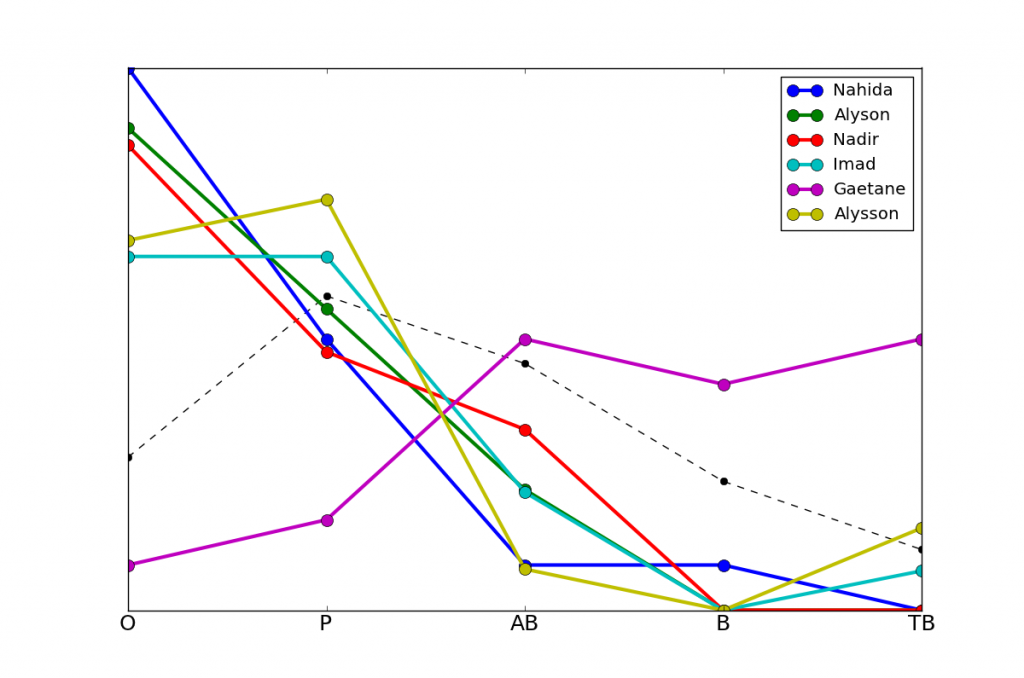
Voici les 30 prénoms associés à la divergence la plus élevée.

Nahida
Alyson
Imad
Nadir
Alysson
Gaetane
Tina
Mariama
Patrice
Madeleine
Aziza
Come
Fatih
Bilel
Manuella
Moussa
Fatma
Giovanni
Abdelkader
Cleo
Elia
Erwin
Isaure
Abdel
Siham
Zelie
Yassin
Mounir
Juliane
Leon

Maintenant, nous pouvons aussi nous intéresser aux prénoms avec la divergence la plus faible, autrement dit les prénoms les plus représentatifs de l'ensemble des candidats. Ces prénoms sont probablement répartis de manière uniforme parmi tous les candidats, sans être associés, par exemple, à une classe sociale particulière qui aurait des résultats très différents de la moyenne. Ainsi, un Valentin ou une Emilie a un profil de résultat tout à fait comparable à la moyenne globale.

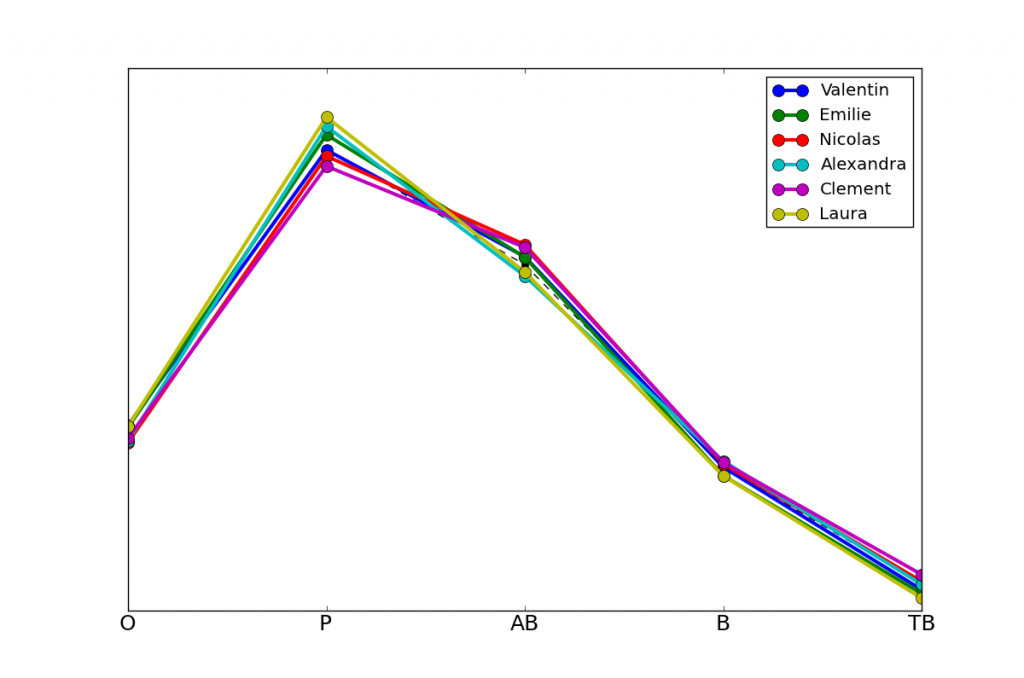
Valentin
Emilie
Nicolas
Alexandra
Clement
Laura
Thomas
Arnaud
Remy
Alexandre
Helene
Hugo
Mario
Bastien
Sebastien
Estelle
Xavier
Romain
Quentin
Eva
Guillaume
Rayan
Vincent
Adrien
Sabine
Ines
Lucas
Sarah
Floriane
Virgile

En conclusion, nous avons donné des méthodes pour trouver les prénoms qui influent le plus (positivement ou négativement) sur le résultat au bac, et à l'inverse pour trouver ceux qui ont le moins d'impact sur le résultat et qui sont le plus proches possible des résultats globaux. Il y a probablement beaucoup d'autres choses à analyser dans ces données.

Méthodes

Données. Les données concernent les résultats de 346851 candidats, toutes séries confondues (générales et technologiques), qui ont au moins eu l'oral et qui ont accepté de rendre disponible publiquement leur résultat. Tous ces candidats portent 18473 prénoms différents. Pour les analyses, nous n'avons considéré que les prénoms portés par au moins 20 candidats, soit 1211 prénoms différents représentant 310145 candidats.

Modélisation. L'ensemble des candidats est noté \(\Omega\), l'ensemble des 1211 prénoms est noté \(E\), l'ensemble des résultats possibles est noté \(F\). L'ensemble \(\Omega\) est muni de la tribu discrète et de la mesure de probabilité uniforme. Les variables aléatoires \(X(\omega)\) et \(Y(\omega)\) sont des variables aléatoires à valeurs dans \(E\) et \(F\), respectivement, et donnant le prénom et le résultat de chaque candidat. Voici les formules utilisées.

• La probabilité de \(y\) est:

  $$ p[y]=\frac{\textrm{card}\left\{\omega \in \Omega \mid Y(\omega)=y\right\}}{\textrm{card}(\Omega)} $$

• La probabilité conditionnelle de \(y\) sachant \(x\) est:

  $$ p[y\mid x] = \frac{\textrm{card}\left\{\omega \in \Omega \mid X(\omega)=x, Y(\omega)=y\right\}}{\textrm{card}\left\{\omega \in \Omega \mid X(\omega)=x\right\}} $$

• L'espérance de \(y\) est:

  $$ E[y]=\sum_{y \in F} y \times p[y] $$

• L'espérance conditionnelle de \(y\) sachant \(x\) est:

  $$ E[y \mid x]=\sum_{y \in F} y \times p[y \mid x] $$

• La divergence de Kullback-Leibler entre la distribution \(p[y]\) et la distribution conditionnelle \(p[y\mid x]\) est:

  $$ D(x)=\sum_{y \in F} p[y \mid x] \times \log\left(\frac{p[y \mid x]}{p[y]}\right) $$