Fréquence des prénoms des candidats au bac 2012

Je poursuis mon analyse des prénoms des candidats au bac cette année (voir billet précédent) en m'intéressant cette fois à la fréquence des différents prénoms portés par les candidats, indépendamment de leurs résultats. Les 346 581 candidats portent 18 473 prénoms différents. Le prénom le plus porté est Camille avec 4 848 candidats. Voici les quelques prénoms les plus utilisés, représentatifs des prénoms à la mode aux alentours de l'année 1994 (nuage réalisé sur Wordle).

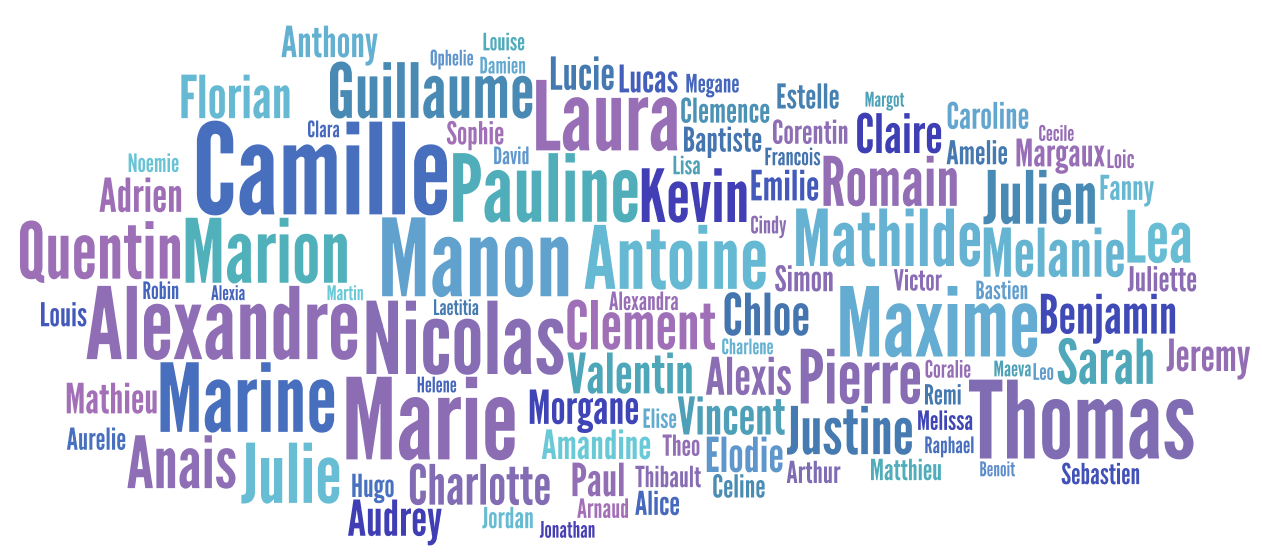
Camille     4848
Marie       4354
Thomas      4134
Manon       4131
Nicolas     3851
Alexandre   3831
Maxime      3720
Laura       3702
Marine      3639
Pauline     3630
Marion      3433
Antoine     3370
Julie       3157
Mathilde    3045
Quentin     3036
Guillaume   2913
Pierre      2872
Julien      2854
Kevin       2835
Lea         2780
Anais       2775
Romain      2621
Clement     2615
Melanie     2576
Justine     2564
Sarah       2398
Florian     2298
Chloe       2256
Charlotte   2172
Valentin    2150

Une observation intéressante est que les prénoms rares sont, paradoxalement, très nombreux. Ainsi, 12 129 prénoms soit 65% de tous les prénoms ne sont portés que par un seul candidat! Mais ces candidats ne représentent que 3.5% du total des candidats. Un nombre important de parents souhaite ainsi donner un prénom unique à leur enfant, souvent d'ailleurs en trouvant des variantes orthographiques originales de prénoms plus classiques. Par exemple, le prénom Zinedine admet comme variantes, entre autres: Zin-Eddine, Zine-Din, Zine-Dine, Zine-Eddine, Zineddine ou Zinnedine. D'ailleurs, les prénoms composés représentent 15% de tous les prénoms (et 2% de tous les candidats).

Poursuivant le raisonnement, on peut s'intéresser au nombre de prénoms portés par 2, 3, 4 candidats ou plus. Cela revient à étudier la distribution des fréquences des prénoms. On obtient alors la courbe suivante.

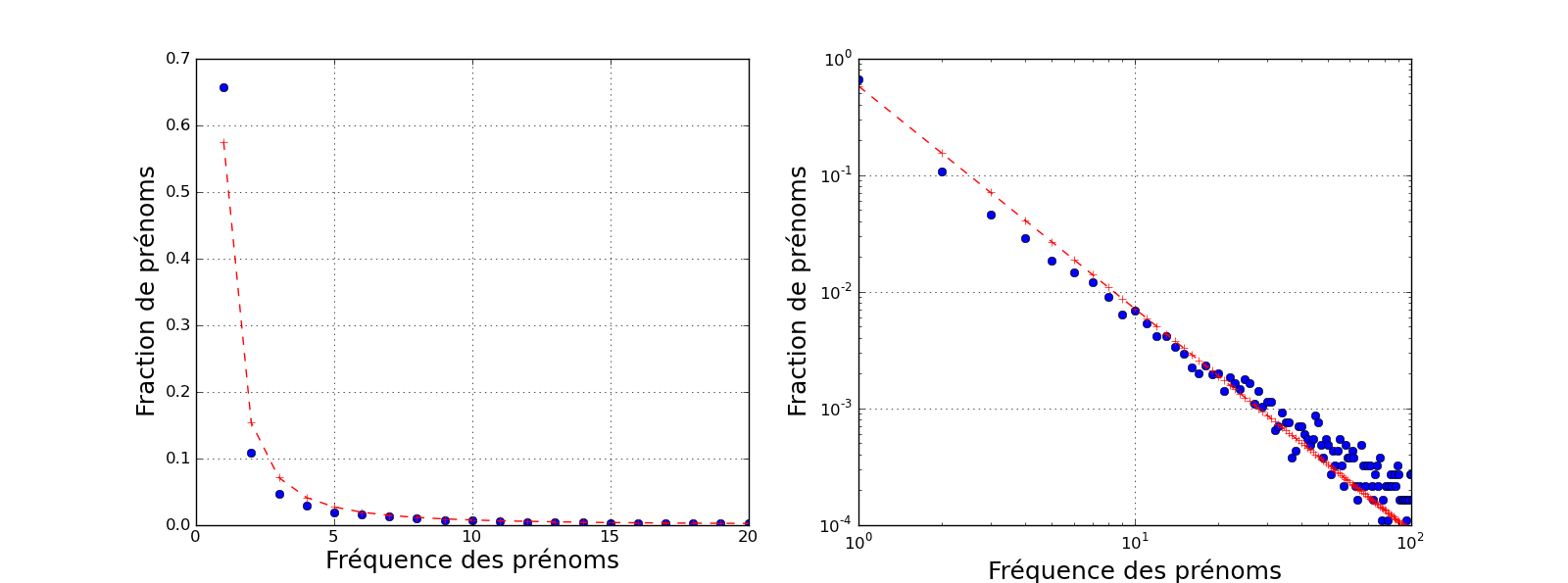
A gauche est représenté la fraction de prénoms qui sont portés par 1, 2, ... jusqu'à 20 candidats (points bleus). Si 65% des prénoms sont portés par un seul candidat, 10% le sont par 2 candidats, 5% le sont par 3, etc. Cette courbe démarre à une valeur importante mais diminue ensuite extrêmement rapidement. Il s'agit d'une propriété caractéristique de nombreux phénomènes et qui porte le nom de "longue traîne". L'utilisation des mots dans une langue donnée, la répartition des richesses, la population dans les villes constituent quelques exemples. Il y a ainsi très peu de villes extrêmement peuplées, et énormément de villes très peu peuplées, de telle sorte qu'environ 20% de toutes les villes représentent 80% de la population. Ou encore, 20% d'une population concentre 80% des richesses. C'est la loi des 80-20, ou principe de Pareto, qui quantifie en quelque sorte certaines inégalités.

Ici, ce principe est approximativement vérifié qualitativement mais non quantitativement: il est en fait plus marqué que la règle des 80-20! Ainsi 80% des candidats sont représentés non pas par 20% des prénoms, mais par 2.5%! Au delà de l'observation d'un grand nombre de prénoms rares, on peut faire celle d'un petit nombre de prénoms très répandus. Ainsi, seuls 0.5% des prénoms servent à nommer la moitié des candidats. De plus, 10% des prénoms représentent 90% des candidats, formant ainsi plutôt une règle des 90-10.

Mathématiquement, on peut constater que la distribution des fréquences des prénoms semble suivre de manière assez approximative une loi de Zipf, typique d'une distribution à longue traîne et satisfaisant à une règle de type 80-20. Cette loi signifie que le nombre de prénoms donné à \(n\) candidats est proportionnel à \(1/n^s\), avec \(s>1\) un paramètre réel (loi de puissance). On constate en effet que la distribution des fréquences des prénoms dans un graphique log-log est approximativement linéaire, suggérant une loi de puissance (voir panneau de droite dans la figure précédente). On peut tenter de faire correspondre une loi de Zipf à ces données, à l'aide d'une méthode d'estimation statistique. En utilisant la méthode du maximum de vraisemblance, on trouve une valeur \(s \simeq 1.9\) pour le paramètre. Cette distribution adaptée aux données est représentée en rouge dans la figure précédente.

Une autre manière de représenter cette distribution est d'afficher le pourcentage de candidats couverts par 1, 2, 3... prénoms, en triant les prénoms par ordre décroissant de fréquence. On obtient le graphique suivant (à droite, échelle log-log) :

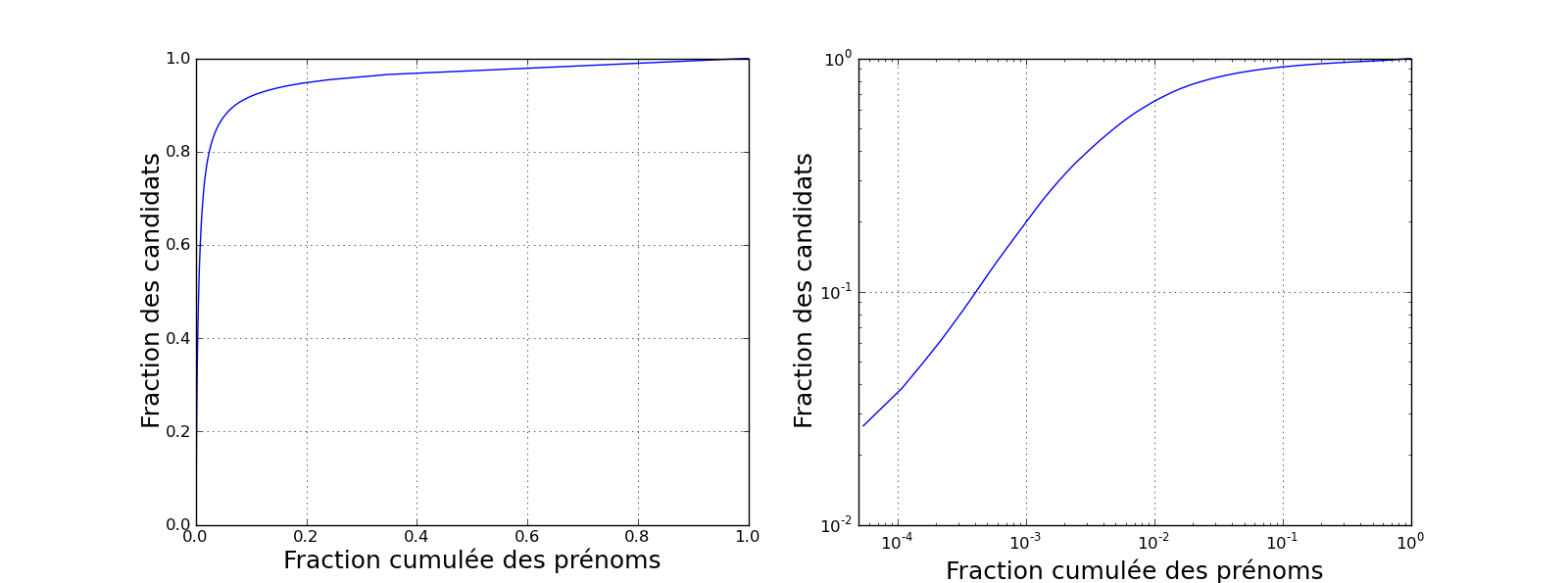
Le "coude" observé à gauche est typique d'une loi de Zipf. De gauche à droite, les prénoms sont classés par fréquence décroissante (le prénom le plus donné d'abord, Camille, puis le second, Marie, etc.). Au fur et à mesure que l'on ajoute ces prénoms, la fraction de candidats représentés augmente très rapidement (partie gauche du coude). Puis viennent les prénoms beaucoup plus rares, portés par un nombre très faible de candidats (partie droite). La courbe croît alors très lentement, le nombre de candidats couverts n'augmentant que d'une fraction infinitésimale à chaque prénom.

La répartition des prénoms est ainsi particulièrement hétérogène, avec d'un côté des prénoms très répandus, et de l'autre côté des prénoms totalement originaux, nouveaux, ou uniques. Y aurait-il deux grandes tendances chez les parents, entre les "traditionalistes" qui souhaiteraient utiliser des prénoms classiques (ou des prénoms d'ascendants familiaux), et les "modernistes" qui souhaiteraient rompre avec le passé et marquer leur originalité? Notons qu'il est possible de concilier les deux tendances, en quelque sorte, en utilisant un prénom du passé en second prénom, comme pour manifester un lien avec les générations précédentes. Par ailleurs, cette tendance observée dans une population très spécifique (une partie des candidats au bac 2012) est-elle la même que celle observée plus généralement dans toute la population? Je laisse le soin aux sociologues d'y répondre.